[原题链接](https://leetcode-cn.com/problems/distribute-candies-to-people/ "原题链接") ## 题干 > 排排坐,分糖果。 >我们买了一些糖果 candies,打算把它们分给排好队的 n = num_people 个小朋友。 >给第一个小朋友 1 颗糖果,第二个小朋友 2 颗,依此类推,直到给最后一个小朋友 n 颗糖果。 >然后,我们再回到队伍的起点,给第一个小朋友 n + 1 颗糖果,第二个小朋友 n + 2 颗,依此类推,直到给最后一个小朋友 2 * n 颗糖果。 >重复上述过程(每次都比上一次多给出一颗糖果,当到达队伍终点后再次从队伍起点开始),直到我们分完所有的糖果。注意,就算我们手中的剩下糖果数不够(不比前一次发出的糖果多),这些糖果也会全部发给当前的小朋友。 >返回一个长度为 num_people、元素之和为 candies 的数组,以表示糖果的最终分发情况(即 ans[i] 表示第 i 个小朋友分到的糖果数)。 ## 解析 ###暴力法 ---------------- 不管怎么来俺就是要莽,莽夫嘛,就是要来一套模拟,搞定。 每次模拟走一次,然后把剩下的存在最后一个访问的小朋友 ###代码 ```java public int[] distributeCandies(int candies, int num_people) { int[] ans = new int[num_people]; int pow = 0; while (candies > 0){ for (int i = 0; i < num_people ; i++) { if (candies >= i + 1 + num_people * pow){ candies -= i + 1 + num_people * pow; ans[i] += i + 1 + num_people * pow; }else { ans[i] += candies; candies = 0; } } pow++; } return ans; } ``` ### 数学小想法(~~莽夫的对立面~~) 使用等差数列的知识,我们可以看出这个完整分配的时候就是一个首项为1,公差为1的等差数列 已知首项、前n项和和公差求项数 Sn = a1 x n+(n x n-1)/2 x d - 求出完整分配的轮数 - 求出最后的杭和烈 - 最后加上剩余的 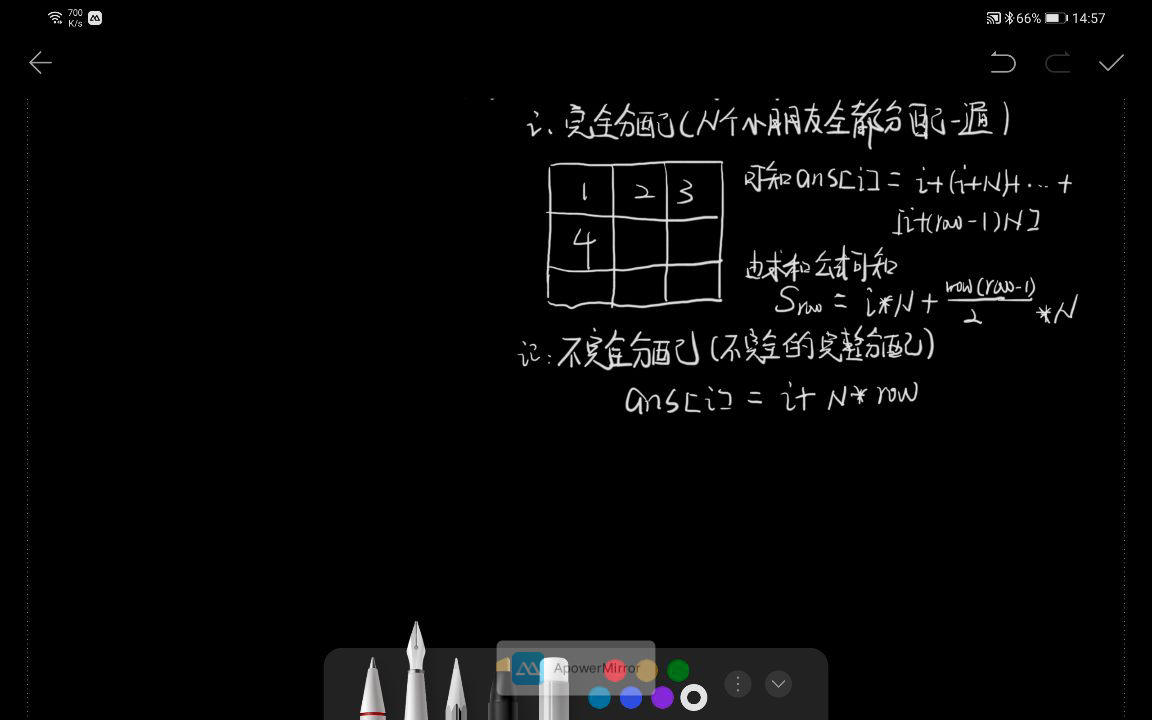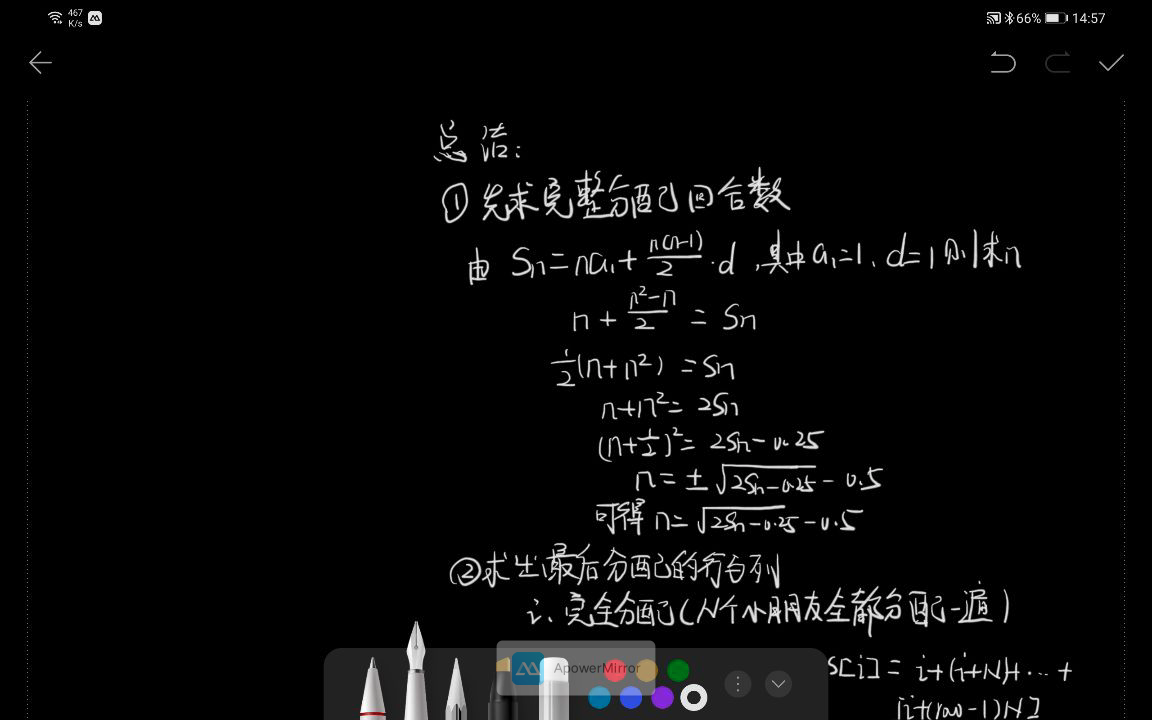 ### 代码 ```java //等差数列求和,Sn = n*a1 + n(n-1)d /2,此处已知Sn a1 d 求 n // n*a1 + (d * n^2 - d * n) / 2 = Sn ==> n = 土sqrt(2 * Sn + 0.25) - 0.5 public int[] distributeCandies(int candies, int num_people) { int[] ans = new int[num_people]; //求出完整分配的项数 int n = (int) Math.floor(Math.sqrt(2*candies + 0.25) - 0.5); //求出完整分配的数量 int sn = n + (n * (n-1)) / 2; //剩余的糖果数 int less = candies - sn; //推算出完整分配的行和列 //rows代表最后一行的行数 int rows = n / num_people; // cols 代表最后一个分配的位置 int cols = n % num_people; for (int i = 0; i < num_people ; i++) { ans[i] = (i + 1) * rows + (int)(rows * (rows - 1) * 0.5) * num_people; //前cols个人分配一份完整的礼物 if (i < cols) ans[i] += i + 1 + rows * num_people; } ans[cols] += less; return ans; } ``` 最后修改:2020 年 05 月 06 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏